Liangyuting Zhang

2D rogue game

OOP Graph Algorithms
2D rogue game

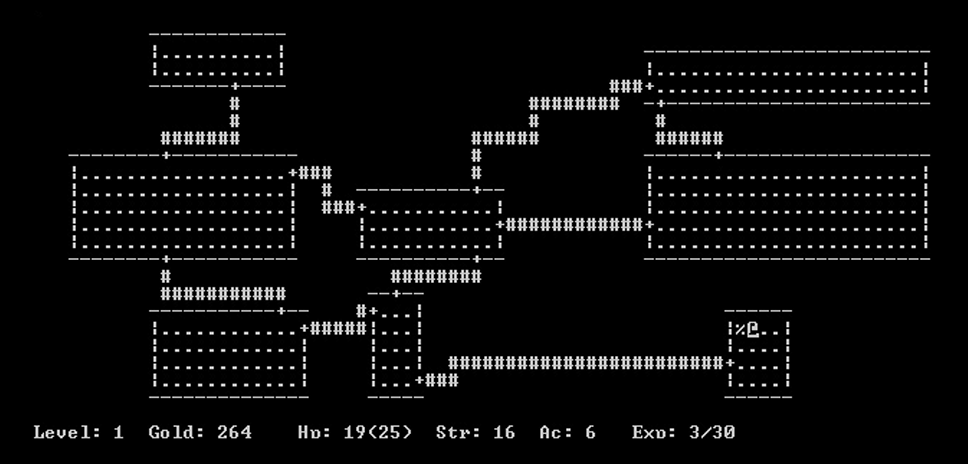
This project was developed as part of the CPT204 Object-Oriented Programming course, focusing on implementing advanced graph algorithms to create intelligent behaviors in a simplified version of the classic 2D game Rogue. The game involves navigating a dungeon, collecting items, and avoiding enemies, with both the player (Rogue) and the enemy (Monster) employing strategic movement. The project highlights the use of pathfinding and cycle detection algorithms to simulate effective pursuit and evasion dynamics.

AI Behavior Demonstration

The following GIFs showcase the dynamic interaction between the Monster and the Rogue, highlighting the effectiveness of the algorithms implemented in this project. Each scenario demonstrates the decision-making process of both agents and the resulting outcomes based on the dungeon layout and available strategies:

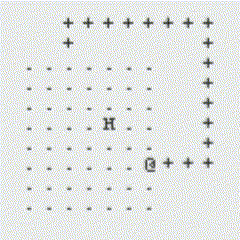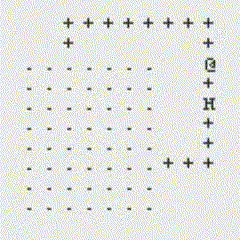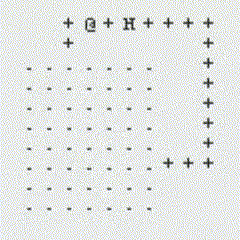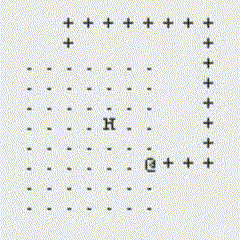
Demo Animation
The Rogue is caught by the Monster due to the lack of a reachable cycle or escape route. The Monster efficiently uses the shortest path to intercept the Rogue.
Demo Animation
The Rogue successfully evades the Monster by entering a reachable cycle. Once inside, the Rogue remains one step ahead of the Monster indefinitely, ensuring safety.
Demo Animation
In this scenario, the Rogue is unable to find a safe cycle and is eventually caught by the Monster. This highlights the Rogue’s survival strategy limitations in a cycle-free dungeon.
Demo Animation
The Rogue leverages the nearest reachable cycle to avoid capture. The Monster attempts to intercept but cannot prevent the Rogue from entering the cycle, resulting in a successful escape.

Path Finding Algorithm

Since the most important part of the game is the path finding algorithm, I will introduce the algorithm in detail.

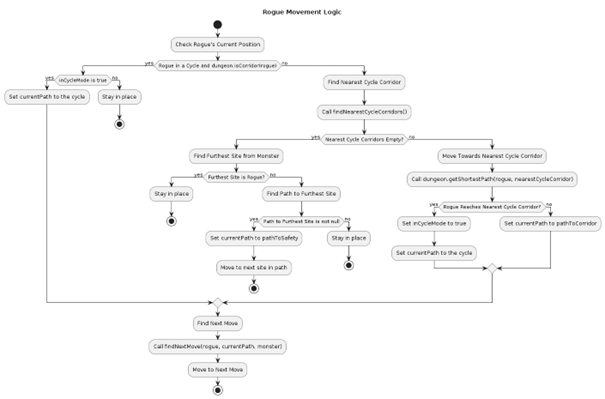
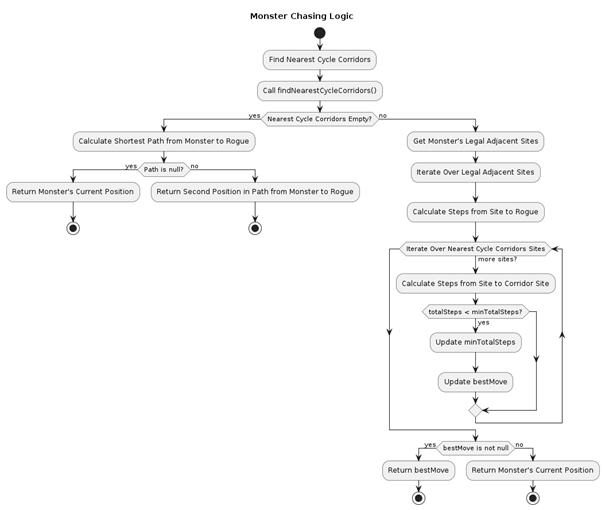
Monster Algorithm: Pursuit Strategies

The Monster’s behavior centers around intelligently tracking and intercepting the Rogue using graph-based strategies:

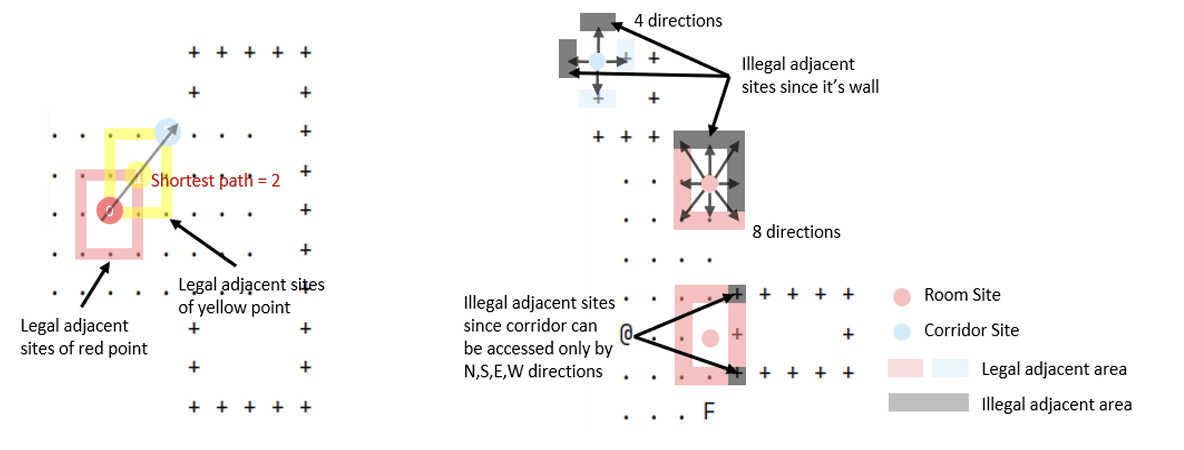
  1. Pathfinding with BFS:
    The Monster uses a Breadth-First Search (BFS) algorithm to calculate the shortest path to the Rogue. This ensures dynamic, layer-by-layer exploration of the dungeon for optimal pursuit.

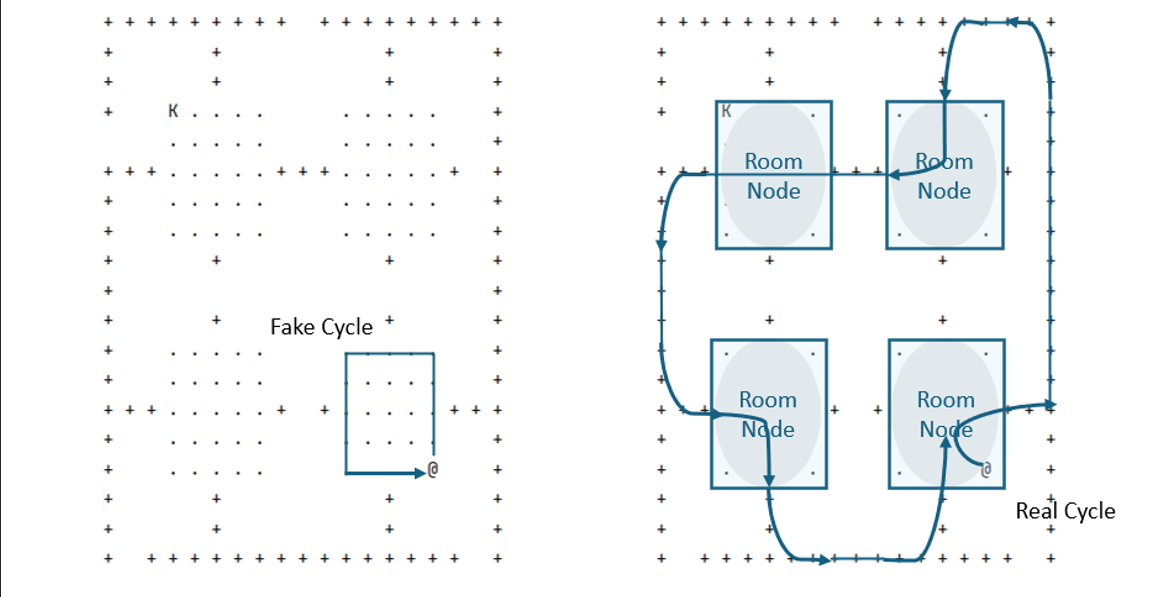
  2. Cycle Detection with DFS:
    The algorithm identifies closed-loop structures (cycles) in the dungeon using Depth-First Search (DFS). These cycles are critical for understanding potential Rogue escape routes. Room areas are abstracted into single nodes to simplify detection and improve computational efficiency.

Example Image
Figure 1. (a) process of BFS for shortest path and (b) legal/illegal adjacent sites
Example Image
Figure 2. Cycle Detection (a) without RoomNode (b) with RoomNode
  1. Hunting Strategies:
    • Shortest Path Pursuit: The Monster directly follows the shortest path to the Rogue.
    • Early Interception: If the Rogue attempts to enter a cycle, the Monster prioritizes blocking the cycle’s entry point, using a heuristic to choose the move that minimizes its distance to both the Rogue and the cycle entry. This strategy disrupts the Rogue’s chances of using cycles to evade capture.
Example Image
Figure 3. the Process Diagram of Monster Chasing Logic

Rogue Algorithm: Evasion Strategies

The Rogue employs adaptive strategies based on the dungeon layout and the Monster’s actions to ensure survival or prolong evasion:

  1. Cycle-Based Strategy (Winning Scenarios):

    • Cycle Identification & Usage: The Rogue identifies reachable cycles in the dungeon where it can evade the Monster indefinitely.
    • Cycle Movement: Once inside a cycle, the Rogue ensures it stays one step ahead of the Monster by maintaining a safe distance within the loop.

  2. Pathfinding for Cycle Entry:
    The Rogue calculates the shortest path to the nearest cycle entry and moves strategically to enter it when threatened.

  3. Survival Strategy (Losing Scenarios):
    If no reachable cycle exists, the Rogue chooses a destination as far from the Monster as possible, maximizing survival time.

  4. Dynamic Adaptation:
    The Rogue’s algorithm continuously evaluates the game state, switching between cycle-based and survival strategies to optimize its moves.

Example Image
Figure 4. the Process Diagram of Rogue Move Logic.

Liangyuting Zhang

Copyright © 2024 Liangyuting Zhang. All Rights Reserved. Modified from free Jekyll theme by Codebase